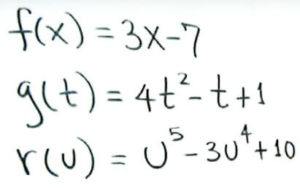Cuando abordamos este tema estamos orientándonos a estudiantes avanzados de matemáticas por lo cual algunos conceptos los damos por conocidos, si bien nunca esta de más recordarlos entendemos que los lectores deben tener algún grado de conocimiento en la materia
Resumen del Contenido
La palabra DOMINIO, en matemática, tiene diversos usos:
- Dominio de definición, es el conjunto de valores para los cuales una determinada función matemática está definida.
- Dominio de integridad, en álgebra, es un anillo (no necesariamente conmutativo ni unitario) que no tiene elementos divisores de cero.
- Dominio (análisis matemático), es un conjunto abierto en el cualquiera dos puntos están unidos mediante una línea poligonal.
- Dominio (geometría), es un conjunto conexo; algunos autores exigen además que sea compacto, otros exigen que sea abierto.
Fuente: wikipedia.org
Seguidamente desarrollaremos los diferentes conceptos para el cálculo del dominio de definición en las funciones.
Para determinar el dominio de una función es importante conocer sus características o limitantes.
Dominio en cálculo de funciones
Definamos los componentes de una función básica:
y=f(x)
- Se define al Dominio de la función (Df)como el conjunto de valores que tomará “x”.
- Y se define el Rango de la función (Rf) como el conjunto de valores que tomará “y”.
Ejemplos de dominios de funciones matemáticas:
- En el primer caso tenemos una función polinómica de primer grado.
- En el segundo caso tenemos una función cuadrática de segundo grado.
- En el tercer caso tenemos una función de quinto grado.
En cualquiera de estos casos el Dominio será un número que pertenece al conjunto de los números reales (ℝ ) porque la variable independiente en cada caso: x, t, u puede tomar cualquier valor que se encuentre comprendido en el rango de estos números.
Para hallar el Dominio en los ejemplos anteriores quedaría de la siguiente manera:
- Df=x∈ℝ
- Dg=t∈ℝ
- Dr=u∈ℝ
Nota: si bien es un concepto básico no está mal recordarlo: se entiende como números reales al conjunto de los números que incluye tanto a los números racionales (positivos, negativos incluido el cero) como a los números irracionales.
Ecuaciones
Por ejemplo una ecuación de 1er grado o grado “0” se representa gráficamente por una línea recta:
Grado 1: línea recta inclinada Grado 1: Línea horizontal Grado 0: Línea vertical
Bien, si observamos el eje “X”, para cualquier valor que se tome existe su equivalencia en el eje “Y”:
Esto ocurrirá tanto en el lado negativo, como el positivo y equivale a decir que una ecuación de 1er grado, no va a tener limitantes.
El dominio siempre será cualquier valor de “X” que pertenezca a los números reales, es decir desde menos infinito hasta infinito.
Esquemáticamente quedaría de la siguiente manera, para una ecuación de 1er grado:
D= X ∈ (- ∞, ∞)
- Dónde D es el Dominio; X es la variable y ∈ es un valor que pertenece a los números reales y ∞ es infinito
En una ecuación de grado 0 solamente existen un valor en “X” que se presenta cuando la línea corta el eje horizontal.

Si al punto de intersección se le da el valor de “a”, es decir “X” vale “a”, la expresión quedará determinada de la siguiente manera:
D = X = a
Conclusión:
- Podemos decir que en toda ecuación de 1er grado el valor del Dominio dependerá del número que le asignemos nosotros mismos dado que están determinados entre infinitos.
- En cambio en una ecuación de grado cero, y en el caso de una línea vertical, el valor del Dominio será el equivalente al valor que le demos a “X”
Polinomios de grado mayor
En este caso se aplica el análisis a polinomios de grado 1,2,3 y sucesivamente, veamos seguidamente como determinar el Dominio:
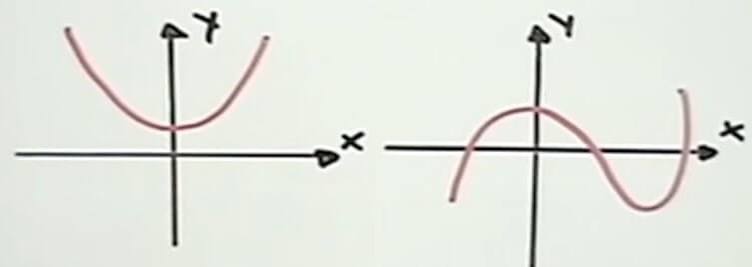
Ecuación 1: F(x) = ax2+bx+c Ecuación 2: F(x) = ax3+bx2+cx+d
Las ecuaciones en estos casos están compuestas por varios valores representados por letras, por lo tanto al momento de encontrar el valor de “X” en estos polinomios, se deberá tener en cuenta que:
- Para cada valor de “X” debe existir un valor en “Y” por lo tanto su Dominio siempre será:
D= X ∈ (- ∞, ∞)
Dónde: D es el Dominio; X es la variable y ∈ es un valor que pertenece a los números reales y ∞ es infinito. Aquí aplica el mismo concepto que las ecuaciones de primer grado el valor de “X” estará limitado o no de acuerdo al valor que le demos a infinito.
Los polinomios no solo están compuestos de sumas y restas ó multiplicaciones, es decir no siempre se podrá aplicar la fórmula del Dominio tal y como lo expresamos anteriormente.
Ciertas operaciones como la división, raíz cuadrada y logaritmo, para los valores de “X” no se podrán resolver o encontrar una solución dentro de los números reales.
Si bien existen más operaciones que tienen restricciones se detallaran aquí las básicas.
División
En el caso de la división se debe tener en cuenta siempre evitar que el denominador sea cero, entonces:
Evitar que x sea cero:
F(x) = 1/x D = {x ∈ ℝ /x#0}
Evitar que x sea 7 o sea x-7=0 ó x=7:
G (x)= 5/x-7 D = {x ∈ ℝ /x#7}
En una ecuación de 2do grado se debe evitar el 0 en el denominador:
M(x)= 2x-1 /x2+x-12 = 2x-1/(x+4)(x-3) D = {x ∈ ℝ /x#-4&x#3}
Raíz cuadrada
En las operaciones con raíz cuadrada para calcular el Dominio hay que evitar que el radicando sea negativo:
Evitar que x sea negativo es decir x≥0
F(x) =√x D = {x ∈ ℝ / x≥0}
Se debe determinar cuándo (X-9) será igual o mayor a 0 es decir X-9≥0:
g(x)=√(x-9) D = {x ∈ ℝ / x≥9}
En este caso el valor de x puede ser 0 por lo tanto se puede resolver si consideramos el concepto del principio de este punto, es decir -X≥0 cuando se multiplica o divide números negativos la desigualdad se invierte o sea X≤0:
m(x)=√(-x) D = {x ∈ ℝ / X≤0}
En este caso 16-x^2 debe ser ≥0, vale decir que cualquier número que se encuentre entre 4 y -4 permitirá resolver la ecuación y calcular el dominio:
n(x)=√(16-x^2 ) D = {x ∈ ℝ / -4≤x 4}
Logaritmos
En el caso de cálculo de dominio en una función logarítmica se debe evitar que la operación dé como resultado 0 ó un número negativo
En este caso se debe evitar que x>0
f(x)=log(x) D = {x∈ℝ / x>0}
La desigualdad que se debe resolver es x+5 de decir: x+5>0 por lo tanto x>-5
g(x)=Ln(x+5) D = {x ∈ ℝ / x>-5}
En este caso el denominador no puede ser 0 cuando x=3, también hay que tener en cuenta que un logaritmo tampoco puede ser negativo, es decir tenemos dos criterios: división y logaritmo. Por lo tanto x no puede ser menor a 3 -> x>3:
n(x)=log 9/ (x-3) D = {x ∈ ℝ/ x>3}
Páginas de referencia
http://www.vitutor.com/fun/5/c_2.html
http://es.wikihow.com/encontrar-el-dominio-de-una-funci%C3%B3n#
http://www.vadenumeros.es/cuarto/dominio-de-funciones.htm
https://www.educatina.com/video?categoria=matematicas&subcategoria=analisis-matematico&rama=estudio-de-funciones&tema=analisis-de-funciones&nombre=dominio-de-una-funcion